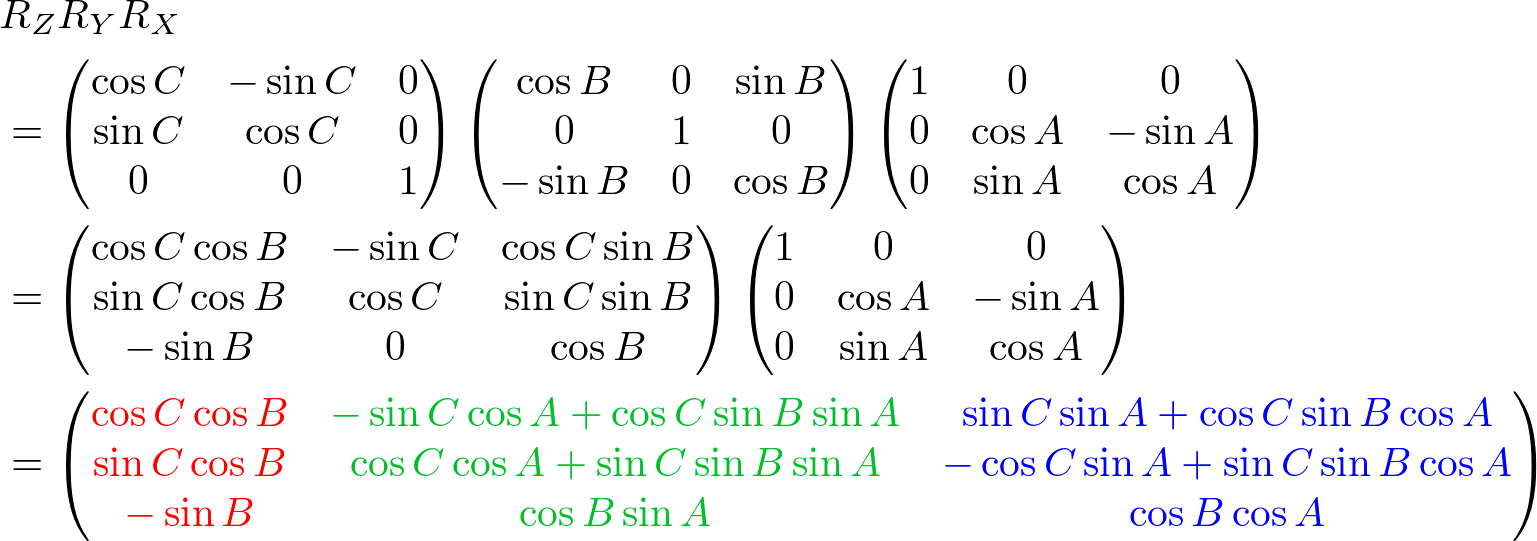
Here, the input is being entered by the user based on a prompt. Step 4 - Iterate over each element of the matrix using a while loop and shift the position of each element by one position to the right using multiple for-loops and store the matrix. Step 2 - Declare an integer matrix namely input_matrix and declare four integer values namely row, column, previous, next. The desired output would be − The matrix after one rotation: Suppose our input is − The matrix is defined as Matrix rotation is shifting the position of each element of the matrix by 1 position towards it’s right or left. A matrix is representation of the elements in rows and columns.
#MOTRIX ROTATIONS HOW TO#
* Method to get the horizontal reflection of the matrix.In this article, we will understand how to rotate matrix elements. * part of the transpose operation in case its not a square matrix. * elements because the physical structure of the matrix may change as a
Take reflection of the transpose against the vertical axis. Take reflection of the resultant matrix against the vertical axis. Take reflection of the matrix against the horizontal axis. Take reflection of the transpose against the horizontal axis. Here is an example of vertical reflection. If the value of N is odd then the position of Column 1 + N/2 remains intact and it is not changed, that is why it is also called vertical reflection through the middle column. This precisely means exchanging one column with the other such that the first column becomes the last, the second column becomes the second last and so on.įor a matrix of dimension M * N there are M rows and N columns and vertical reflection means Column N is exchanged with Column 1, Column N-1 is exchange with Column 2 so on. Here is an example of horizontal reflection. If the value of M is odd then the position of row 1 + M/2 remains intact and it is not changed, that is why it is also called horizontal reflection through middle row. This precisely means exchanging one row with the other such that the first row becomes the last, the second row becomes the second last and so on.įor a matrix of dimension M * N there are M rows and N columns and horizontal reflection means Row M is exchanged with Row 1, Row M-1 is exchange with Row 2 so on. In simple words, if we can exchange each column with each of the rows in order (1st column with first row, second column with second row and so on.) then at the end of the iteration we will get the transpose of the matrix. The red boundaries (rows) in the matrix A becomes the column in A T and the blue boundaries (columns) in matrix B becomes the row in B T. Here is an image to demonstrate the transpose of a given matrix. So, let us first talk about transpose.Ī transpose of a matrix A(M * N) is represented by A T and the dimensions of A T is N * M. Prerequisites – Matrix RotationsĪ necessary prerequisite for the matrix rotations is to have knowledge about matrix transpose. Rotation matrices are used in two senses: they can be used to rotate a vector into a new position or they can be used to rotate a coordinate basis (or coordinate system) into a new one. 
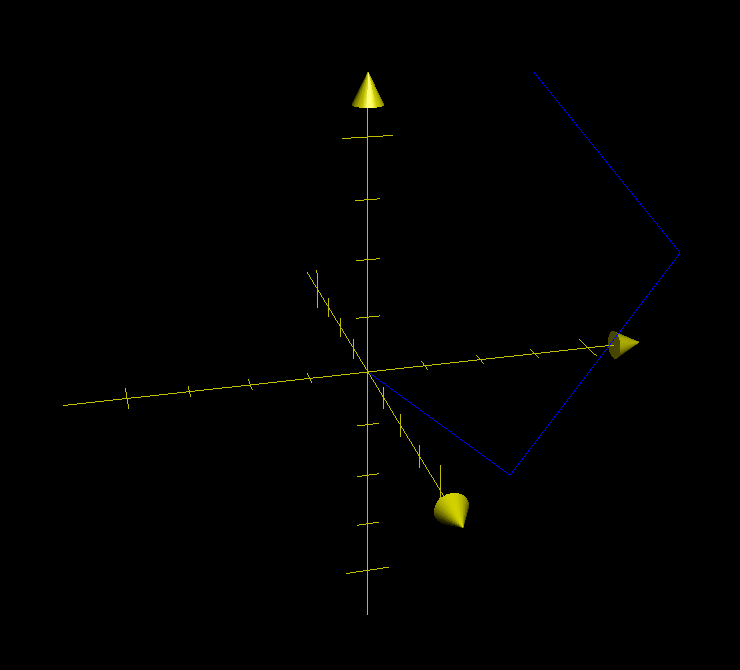
In transforming vectors in three-dimensional space, rotation matrices are often encountered. Depending on the degrees by which we want to rotate, the permutations of the operations may vary. Rotation matrices are used to rotate a vector into a new direction. Just for a formal definition, I would say that matrix rotation is a structural re-arrangement of the rows and columns of the matrix and it is achieved by a sequence of operations on the matrix as a whole. This can only be explained by nice diagrams. A number from the set (90, 180, ,270) by which we need to rotate the matrix.įor simplicity we will consider a matrix to be a 2 dimensional array of integers.We are trying to solve the problem of matrix rotations where the inputs are as follows: This is a very famous interview question and has been asked numerous times. Problem Definition – Matrix Rotation (by 90, 180, 270 degrees)
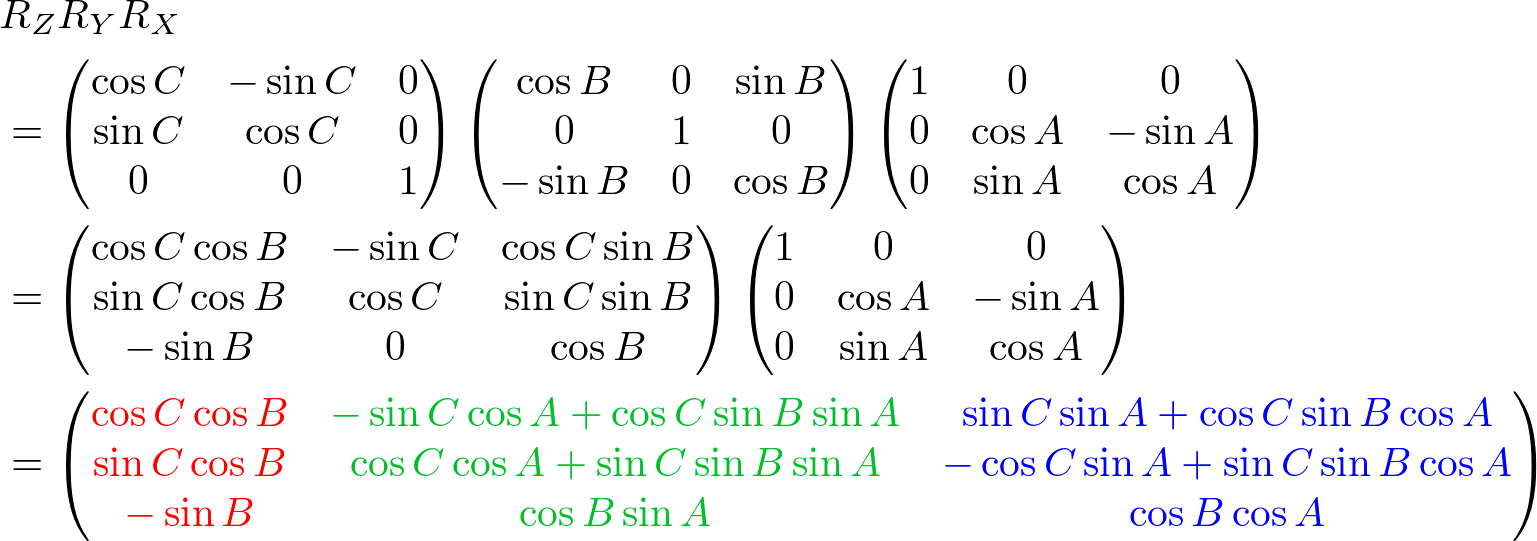
0 kommentar(er)
